Introduction
The Short-Time Fourier Transform (STFT) is a powerful signal processing technique that allows us to analyze how the frequency content of a signal changes over time. When taking the Fourier Transform of a signal, we obtain information about the frequency components of a signal but lose all time-domain information. STFT offers a compromise between time and frequency resolution. This makes it an invaluable tool in many applications where both temporal and spectral information are crucial.
Background on Fourier Transforms
Before diving into STFT, it's essential to understand the basics of Fourier Transforms. The Fourier Transform (FT) is a mathematical technique that decomposes a signal into its constituent frequencies. For a continuous-time signal x(t), the Fourier Transform is defined as:
Where X(f) represents the frequency domain representation of the signal x(t).
While the Fourier Transform is incredibly useful for analyzing the frequency content of stationary signals (signals whose properties do not change over time), it falls short when dealing with non-stationary signals, which are common in real-world applications.
Short-Time Fourier Transform Explained
Basic Principle
The Short-Time Fourier Transform works by dividing a longer time signal into shorter segments of equal length and then computing the Fourier Transform separately on each segment. This approach allows us to analyze how frequency content changes over time.
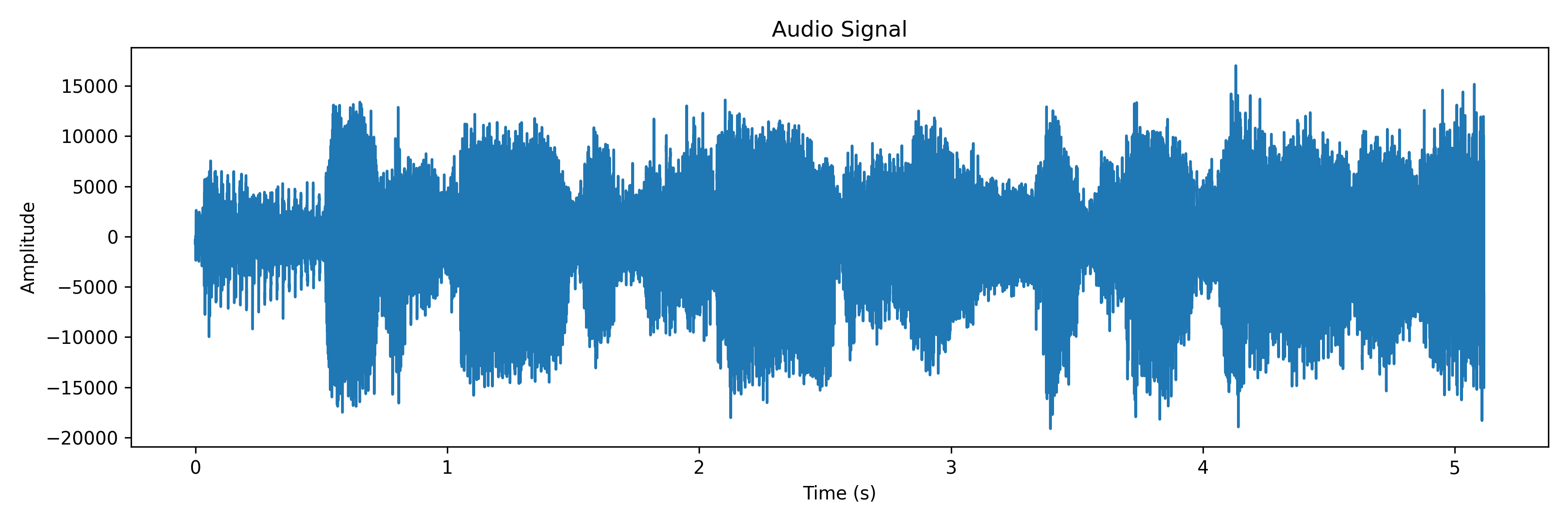
Here is a random 5 second clip from Don't Stop Believin' by Journey.
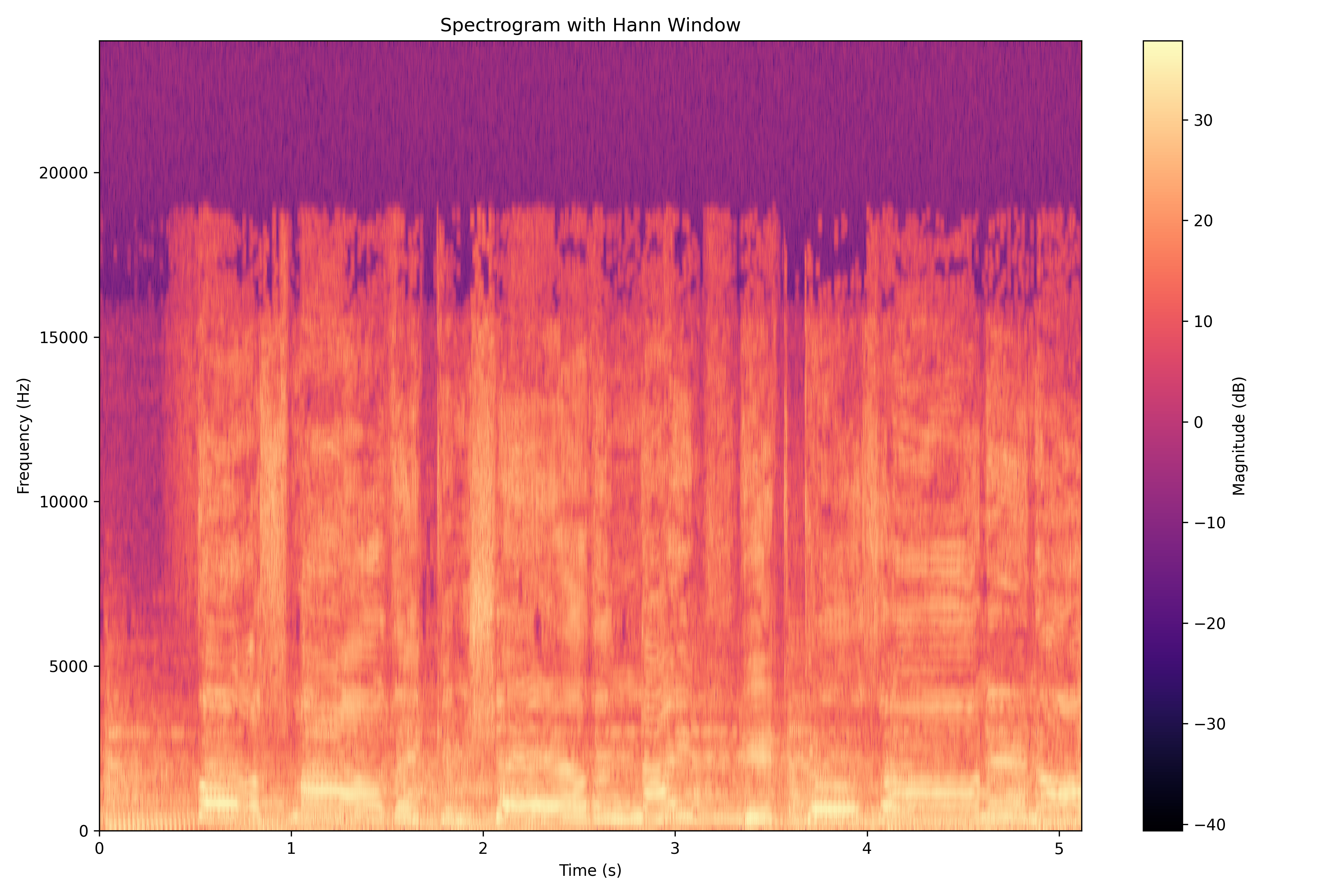
Here is the Short-Time Fourier Transform of the signal (actually, the spectrogram in dB. More on that later). The x-axis represents time, the y-axis represents frequency, and the color represents the magnitude of the frequency components. There are 256 samples on each FFT and a 50% overlap rate. We overlap the FFTs to get a smoother spectrogram.
As you can see, the STFT provides a time-frequency representation of the signal, allowing us to observe how the frequency content evolves over time.
We can clearly see dashed lines in certain parts of the spectrogram. That is the piano! It is so cool that we can see what the piano is playing by looking at the Short Time Fourier Transform of the signal.
Windowing
A crucial concept in STFT is windowing. Instead of abruptly cutting the signal into segments, which can introduce artifacts, we multiply the signal by a window function. Common window functions include Hamming, Hann, and Gaussian windows. The choice of window function affects the trade-off between time and frequency resolution.

As you can see, the windowing function smooths out the abrupt transitions between segments and removes artifacts, resulting in a more coherent spectrogram. The choice of window function can significantly impact the quality of the STFT.
Mathematical Formulation
For a discrete-time signal x[n], the STFT is defined as:
Where:
- w[n] is the window function
- m is the time index of the center of the window
- ω is the angular frequency
How does it work
- Divide the signal into overlapping segments
- Apply a window function to each segment
- Compute the Fourier Transform of each segment
- Stack the results to form the STFT
Time-Frequency Resolution Trade-off
STFT faces a fundamental trade-off between time and frequency resolution, governed by the Heisenberg uncertainty principle. A narrow window gives good time resolution but poor frequency resolution, while a wide window does the opposite. This trade-off is inherent to STFT and cannot be eliminated, only balanced based on the specific application requirements.

Left has better time resolution, and right has better frequency resolution.
Spectrogram
The STFT is often visualized as a spectrogram, which is a 2D representation of the signal's time-frequency content. The x-axis represents time, the y-axis represents frequency, and the color represents the magnitude of the frequency components. To obtain a spectrogram, we typically convert the magnitude of the STFT to decibels (dB) to enhance visualization.
STFT -> 10*log(abs(STFT))
My Implementation
Here is a simple implementation of the STFT in C. The code computes the STFT of a test signal consisting of two sinusoidal components and prints the results to the console.
FFT
For the FFT implementation, I used the Cooley-Tukey algorithm, which is a widely used method for computing the Discrete Fourier Transform (DFT) efficiently. The Cooley-Tukey algorithm is based on the divide-and-conquer strategy and is particularly well-suited for computing the DFT of sequences with a length that is a power of 2.
The Cooley-Tukey algorithm works by recursively dividing the input sequence into smaller subsequences and combining the results to compute the DFT of the original sequence. The algorithm exploits the periodicity of the DFT to reduce the number of arithmetic operations required to compute the DFT.
//Created by: Arda Bulut
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define PI 3.14159265358979323846
/*
Complex number structure
* real: real part of the complex number
* imag: imaginary part of the complex number
*/
typedef struct {
double real;
double imag;
} Complex;
// Complex number operations
Complex complex_add(Complex a, Complex b) {
return (Complex){a.real + b.real, a.imag + b.imag};
}
Complex complex_sub(Complex a, Complex b) {
return (Complex){a.real - b.real, a.imag - b.imag};
}
Complex complex_mul(Complex a, Complex b) {
return (Complex){a.real * b.real - a.imag * b.imag, a.real * b.imag + a.imag * b.real};
}
Complex complex_exp(double x) {
return (Complex){cos(x), sin(x)};
}
void fft(Complex* x, int n) {
/* Fast Fourier Transform / Radix-2 FFT Implementation
* x: input array of complex numbers
* n: number of elements in x
* Radix-2 algorithm is a member of the family of Fast Fourier transform (FFT)
* algorithms. Radix-2 FFT is the simplest and most common form of
* the Cooley–Tukey algorithm. It computes separately the DFTs of the even-indexed inputs (x0, x2 ,..., xN−2)
* and of the odd-indexed inputs (x1, x3,..., xN−1), and then combines those two results to
* produce the DFT of the whole sequence.
*/
if (n <= 1) return; // end of recursion
// initialize even and odd indice objects
Complex* even= (Complex*)malloc(n/2 * sizeof(Complex));
Complex* odd= (Complex*)malloc(n/2 * sizeof(Complex));
// split x into even and odd indices
for (int i= 0; i < n/2; i++) {
even[i]= x[2*i];
odd[i]= x[2*i+1];
}
//recursive fft
fft(even, n/2);
fft(odd, n/2);
// DFT
for (int i= 0; i < n/2; i++) {
Complex t= complex_mul(complex_exp(-2 * PI * i / n), odd[i]);
x[i]= complex_add(even[i], t);
x[i + n/2]= complex_sub(even[i], t);
}
free(even);
free(odd);
}
void hann_window(double* window, int n) {
/*
* Hann window function
* window: output array for the window
* n: number of elements in the window
*
* The Hann window is a taper formed by using a raised cosine or sine-squared with ends that touch zero.
* It is defined as w(n) = 0.5 - 0.5 * cos(2 * pi * n / N) where 0 <= n <= N.
* The Hann window is used to minimize the spectral leakage when performing a Fourier Transform on a signal.
*/
for (int i= 0; i < n; i++) {
window[i]= 0.5 * (1 - cos(2 * PI * i / (n)));
}
}
Complex** stft(double* signal, int signal_length, int window_size, int hop_size, int* num_frames, int* num_bins) {
/* Short-Time Fourier Transform (STFT)
* signal: input signal
* signal_length: number of elements in the signal
* window_size: size of the window
* hop_size: number of samples between the start of consecutive windows
* num_frames: number of frames in the STFT result
* num_bins: number of frequency bins in the STFT result
*
* STFT is a sequence of Fourier transforms of a windowed signal. The signal is divided into
* overlapping frames, and the Fourier transform of each frame is computed.
*
* https://brianmcfee.net/dstbook-site/content/ch09-stft/STFT.html
*/
// Compute the number of frames
*num_frames= 1 + (signal_length - window_size) / hop_size;
*num_bins= window_size / 2 + 1;
// Initialize the output array
Complex** stft_result= (Complex**)malloc(*num_frames * sizeof(Complex*));
for (int i= 0; i < *num_frames; i++) {
stft_result[i]= (Complex*)malloc(*num_bins * sizeof(Complex));
}
// We'll use Hanning window here
double* window= (double*)malloc(window_size * sizeof(double));
hann_window(window, window_size);
// Populate each frame's DFT results
for (int k= 0; k < *num_frames; k++) {
// Slice the k'th frame, apply a window, and take its DFT
Complex* frame= (Complex*)malloc(window_size * sizeof(Complex));
for (int i= 0; i < window_size; i++) {
if (k * hop_size + i < signal_length) {
frame[i]= (Complex){signal[k * hop_size + i] * window[i], 0};
} else {
frame[i]= (Complex){0, 0};
}
// frame[i] = complex_mul(frame[i], (Complex){window[i], 0});
}
fft(frame, window_size);
for (int i= 0; i < *num_bins; i++) {
stft_result[k][i]= frame[i];
}
free(frame);
}
free(window);
return stft_result;
}
// Helper function to free STFT result
void free_stft_result(Complex** stft_result, int num_frames) {
for (int i= 0; i < num_frames; i++) {
free(stft_result[i]);
}
free(stft_result);
}
// Simple unit test for FFT
void test_fft() {
Complex x[]= {{1, 0}, {5, 0}, {2, 0}, {6, 0}};
int n= 4;
fft(x, n);
//[14.+0.j -1.+1.j -8.+0.j -1.-1.j]
Complex expected[]= {{14, 0}, {-1, 1}, {-8, 0}, {-1, -1}};
for (int i= 0; i < n; i++) {
if (fabs(x[i].real - expected[i].real) > 1e-6 || fabs(x[i].imag - expected[i].imag) > 1e-6) {
printf("FFT test failed\n");
return;
}
}
printf("FFT test passed\n");
}
double** spectrogram(double* signal, int signal_length, int window_size, int hop_size, int* num_frames, int* num_bins) {\
/* Spectrogram
* signal: input signal
* signal_length: number of elements in the signal
* window_size: size of the window
* hop_size: number of samples between the start of consecutive windows
* num_frames: number of frames in the STFT result
* num_bins: number of frequency bins in the STFT result
* Spectrogram is a visual representation of the spectrum of frequencies of a signal as it varies with time.
* It is a 2D plot of the magnitude of the Fourier transform of a windowed signal as a function of time.
* Spectrograms are calculated by taking the magnitude of the STFT.
*/
// Compute the STFT
Complex** stft_result = stft(signal, signal_length, window_size, hop_size, num_frames, num_bins);
// Compute the magnitude spectrogram
double** spectrogram = (double**)malloc(*num_frames * sizeof(double*));
for (int i = 0; i < *num_frames; i++) {
spectrogram[i]= (double*)malloc(*num_bins * sizeof(double));
}
for (int i= 0; i < *num_frames; i++) {
for (int j= 0; j < *num_bins; j++) {
spectrogram[i][j]= sqrt(stft_result[i][j].real * stft_result[i][j].real + stft_result[i][j].imag * stft_result[i][j].imag);
}
}
// Free the STFT result
free_stft_result(stft_result, *num_frames);
return spectrogram;
}
// Simple unit test for STFT
void test_stft() {
double signal[]= {1, 2, 1, 2, 1, 2, 1, 2};
int signal_length= 8;
int window_size= 4;
int hop_size= 2;
int num_frames, num_bins;
Complex** result= stft(signal, signal_length, window_size, hop_size, &num_frames, &num_bins);
if (num_frames = 3 || num_bins = 3) {
printf("STFT test failed: incorrect dimensions\n");
free_stft_result(result, num_frames);
return;
}
Complex expected[]= {{3, 0}, {-1, 0}, {-1, 0}};
for (int i= 0; i < num_frames; i++) {
for (int j= 0; j < num_bins; j++) {
if (fabs(result[i][j].real - expected[j].real) > 1e-6 || fabs(result[i][j].imag - expected[j].imag) > 1e-6) {
printf("STFT test failed\n");
free_stft_result(result, num_frames);
return;
}
}
}
printf("STFT test passed\n");
}
int main() {
// Run unit tests
test_fft();
test_stft();
return 0;
}